Una generica retta ha equazione esplicita:

y= mx + q

dove m è il coefficiente angolare della retta, cioè:

  se q=0

e q è l'ordinata del punto di incontro della retta con l'asse y, cioè quando x=0, cioè:

y = q se x=0

Se P (x₁;y₁) appartiene alla retta r vuol dire che soddisfa l'equazione della retta; quindi:

y₁= mx₁ + q

da cui q =  y₁ - mx₁

sostituisco q in:

y= mx + q

ed ottengo:

y= mx +  y₁ - mx₁

raccolgo a fattor comune m ed ottengo:

y= m(x - x₁) +  y₁

Essa è l'equazione della retta passante per il punto P (x₁;y₁)

Spesso y₁ lo si porta al primo membro e si ha:

y - y₁= m(x - x₁)

Se si indicano le coordinate con  P (x₀;y₀)

 si ha:

y - y₀ = m(x - x₀)

Le rette passanti per un punto P (x₁;y₁) sono infinite; esse formano un fascio proprio di rette. Il fascio improprio di rette si ha quando le rette sono parallele tra loro.

Rette parallele

Abbiamo già detto che il coefficiente angolare:

nella equazione esplicita della retta:

y=mx + q

grafico di tre rette parallele con m=0,5 e a=26,56°

quindi, tutte le rette che hanno lo stesso coefficiente angolare m, sono parallele tra loro.

Se poi voglio che una retta r' sia parallela ad un altra retta r e passi per un punto P (x₁;y₁) devo scrivere l'equazione della retta passante per quel punto, cioè:

y= m(x - x₁) +  y₁

ed imporre che abbia lo stesso coefficiente angolare m della prima retta r.

Esempio

grafico della retta -0,5x+y-3=0

L'equazione è:

-0,5x + y - 3 = 0

Voglio scrivere l'equazione della retta che passi per il punto

P₁ (5;0)

non appartenente alla prima retta, ma che sia parallela ad essa.

Mi trovo m dalla equazione:

-0,5x + y - 3 = 0

isolando la y ottengo:

y  = 0,5x + 3

Il coefficiente angolare delle due rette è:

m=0,5

Scrivo l'equazione della retta che passa per il punto P₁ (x₁;y₁)

y= m(x - x₁) +  y₁

al posto di m metto il valore di 0,5 ed ottengo:

y= 0,5(x - x₁) +  y₁

Sostituisco le coordinate di P₁ (5;0) ed ottengo:

y= 0,5(x - 5) +  0

da cui:

y= 0,5x - 2,5

Disegno, per conferma, le due rette, usando la pagina: Disegna grafici e segmenti

ed ottengo:

grafico delle due rette parallele con m=0,5 e con una in P1 (5;0)

Rette ortogonali

Consideriamo due rette r ed s, tra loro ortogonali.

grafico di due rette ortogonali con m=1,33 e m'=-0,75)

Supponiamo che passino per l'origine O degli assi ortogonali. La retta r ha coefficiente angolare m; la retta s ha coefficiente angolare m'.

Costruiamo un triangolo rettangolo in O; vertice A(1;m) e vertice B(1;m').

L'altezza relativa alla ipotenusa AB è il segmento OH, di lunghezza 1 per costruzione.

L'altezza di un triangolo rettangolo, relativa alla ipotenusa, è media proporzionale con le proiezioni dei due cateti sulla ipotenusa, in base al 2° Teorema di Euclide. Ruoto gli assi di 90°, per vedere meglio.

grafico ruotato di 90° di due rette ortogonali con m=1,33 e m'=-0,75

Cioè:

BH:OH=OH:HA

Voglio trovare il rapporto tra i due coefficienti angolari m ed m'. Noto che:

BH=m'

HA=m

OH=1

Poiché, nella proporzione, il prodotto dei medi è uguale al prodotto degli estremi, ho:

OH·OH=BH·HA

da cui

1·1=m' · m

da cui mi ricavo m':

Il ragionamento l'ho fatto sulle lunghezze dei segmenti, cioè ho trascurato i segni dei coefficienti m ed m'. Ricordando che m è positivo se la retta si trova nel primo e terzo quadrante; m è negativo se la retta si trova nel secondo e quarto quadrante; poiché r ha m positivo, mentre la retta s ha m' negativo, mettendo i segni ottengo:

Cioè una retta è ortogonale all'altra se i rispettivi coefficienti angolari sono uno il reciproco dell'altro, ma cambiati di segno.

La dimostrazione l'abbiamo fatta considerando due rette r ed s, che passano per l'origine. Ma è valida per qualunque posizione di due rette ortogonali;

grafico di due rette ortogonali con m=1,33 e m'=-0,75 ma con l'aggiunta di q e q'

infatti traslando, cioè spostando le due rette ortogonali in un altro punto del piano, ottengo sempre rette parallele tra loro ed ortogonali tra di loro. Ricordiamo che q rappresenta l'ordinata del punto di intersezione di una retta con l'asse delle y. Nella dimostrazione q e q' erano uguali a zero, in quanto le due rette ortogonali passavano entrambe per l'origine degli assi O.

Esempio

grafico della retta -0,5x+y-3=0

L'equazione è:

-0,5x + y - 3 = 0

Voglio scrivere l'equazione della retta che passi per il punto

P₁ (5;0)

non appartenente alla prima retta, ma che sia appartenente ad una retta ortogonale ad essa.

Mi trovo m dalla equazione:

-0,5x + y - 3 = 0

isolando la y ottengo:

y  = 0,5x + 3

da cui:

m=0,5

Il coefficiente angolare di una retta ortogonale alla prima è:

metto i valori ed ottengo:

m'=-2

Scrivo l'equazione della retta che passa per il punto P₁ (x₁;y₁)

y= m(x - x₁) +  y₁

al posto di m metto il valore di -2 ed ottengo:

y= -2(x - x₁) +  y₁

Sostituisco le coordinate di P₁ (5;0) ed ottengo:

y= -2(x - 5) +  0

da cui:

y= -2x +10

Disegno, per conferma, le due rette, usando la pagina: Disegna grafici e segmenti

ed ottengo:

grafico di due rette ortogonali con m=0,5 e m'=-2 con una nel punto P1 (5;0)

Retta passante per due punti

Siano dati due punti nel piano.

vogliamo scrivere l'equazione della retta passante per i due punti.

Indichiamo con x₁ ed y₁ le coordinate di P; cioè:

P (x₁;y₁)

Indichiamo con x₂ ed y₂ le coordinate di Q; cioè:

Q (x₂;y₂)

Se usiamo l'equazione esplicita della retta:

y=mx + q

ci serve calcolare il coefficiente angolare m e q, ed imporre che la retta passi per uno dei due punti.

Passando la retta tra i due punti saranno verificate contemporaneamente le due equazioni:

y₁=mx₁ + q

e

y₂=mx₂ + q

Sottraiamo, membro a membro, dalla seconda equazione la prima equazione. Otteniamo:

y₂-y₁ = mx₂ + q - mx₁- q = mx₂ - mx₁ = m(x₂ -x₁)

cioè:

y₂-y₁ = m(x₂ - x₁)

da cui:

m è, quindi, il coefficiente angolare della retta passante per i punti P (x₁;y₁) e Q (x₂;y₂)

Scriviamo l'equazione della retta r, avente coefficiente angolare m e passante per il primo punto P (x₁;y₁)

L'equazione della retta passante per il punto P (x₁;y₁) è:

y - y₁= m(x - x₁)

sostituisco:

ed ottengo:

Questa è l'equazione della retta passante per i punti P (x₁;y₁) e Q (x₂;y₂)

Essa non è valida se la retta è parallela all'asse delle ordinate, in quanto si annulla il denominatore della frazione, cioè:

x₂-x₁=0

avendo i due punti la stessa ascissa, cioè x₁=x₂.

grafico della retta y=x1

In tal caso l'equazione della retta passante per i due punti è:

y=x₁

L'equazione della retta passante per due punti può anche essere scritta in questo modo:

oppure in quest'altro modo, isolando la y:

Esempio

punti che appartengono ad una retta di cui non conosco l'equazione

Scrivere l'equazione della retta passante per i punti P(3;2) e Q(6;6)

Posso usare questa equazione della retta passante per due punti:

Metto i valori delle coordinate dei due punti, ed ottengo:

da cui:

da cui:

Quindi:

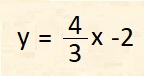
che è l'equazione della retta cercata.

retta passante per i punti P(3;2) e Q(6;6)

Verifico che passi per i due punti.

Nel punto P(3;2) ho

Quindi è verificata, in quanto y=2 nel punto  P(3;2)

Nel punto Q(6;6) ho

Quindi è verificata, in quanto y=6 nel punto  Q(6;6)

Verifico l'incontro con gli assi x ed y.

Se y=0 ho:

da cui:

Controllo sul grafico:

Infatti il punto A(1,5;0) appartiene alla retta.

Per x=0 avrò y=-2